指数平滑法による予測
FORECAST.ETS.CONFINT 指数平滑法を利用して予測された値の信頼区間を求める
対応バージョン：
［タイムライン］を元に［目標期日］の値を予測したとき、［信頼レベル］で指定された信頼区間を求めます。季節によって変動がある場合は［季節性］の指定や、欠測値がある場合には［補間］の指定ができます。元のデータに同じ期の値が複数ある場合には［集計］の指定もできます。予測にはETS（三重指数平滑法）アルゴリズムのAAAバージョンと呼ばれる方法が使われます。
入力方法と引数
FORECAST.ETS.CONFINT
| 目標期日 | 予測値を求める期を指定します。 | |
|---|---|---|
| 値 | タイムラインに対応する値（予測に使う元の値）を指定します。 | |
| タイムライン | 年度や日付など、［値］が得られた期を指定します。 | |
| 信頼レベル | 信頼区間の信頼レベルを指定します。0より大きく、1より小さい値を指定します。省略した場合は95%が指定されたものとみなされます。 | |
| 季節性 | 季節性の変動がある場合に、周期を指定します。1を指定するか省略すると季節性は自動的に計算されます。0を指定すると季節性がないものと見なされます。8760までの値が指定できます。 | |
| 補間 | 欠測値がある場合に1を指定すれば自動的に補間されます。0を指定すると欠測値を0とします。省略すると1が指定されたものと見なされます。全体の30%までは欠測値の補間が行われます。 | |
| 集計 | タイムラインに同じ期がある場合、［値］を集計します。以下の方法が指定でき、（ ）内に記述した関数と同じ方法で集計を行います。省略した場合は集計を行いません。 | |
| 1 | 平均（AVERAGE） | |
| 2 | 数値の個数（COUNT） | |
| 3 | データの個数（COUNTA） | |
| 4 | 最大値（MAX） | |
| 5 | 中央値（MEDIAN） | |
| 6 | 最小値（MIN） | |
| 7 | 合計（SUM） | |
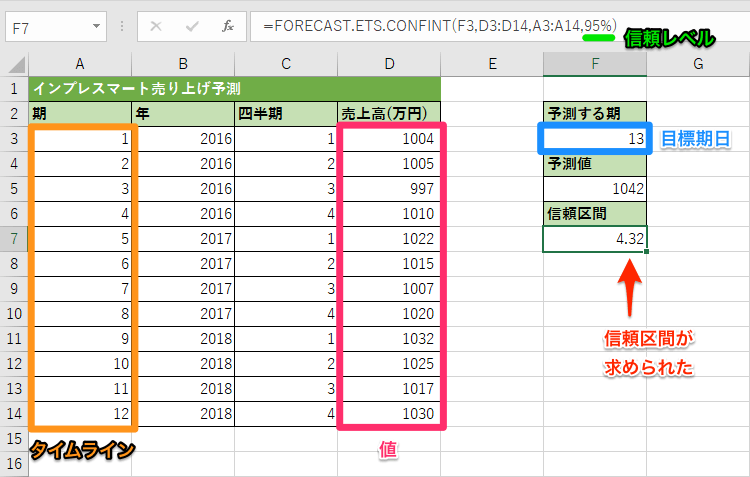
使用例1四半期ごとの売上高を元に2019年第1四半期の売上高を予測し、その信頼区間を求める
=FORECAST.ETS.CONFINT(F3,D3:D14,A3:A14,95%)
上記はセルF7に入力されている数式です。セルF3に入力されている目標期日の売上高を予測し、その信頼区間を返します。セル D3〜D14に入力されている［値］が売上高で、それに対する［タイムライン］がセルA3〜A14に入力されています。セルF5には
=FORECAST.ETS(F3,D3:D14,A3:A14)
が入力されており、2016年から2018年までの四半期ごとの売上高を元に2019年第1四半期の売上高が予測されています。したがって、この例では95%信頼区間は1042±4.32となります。
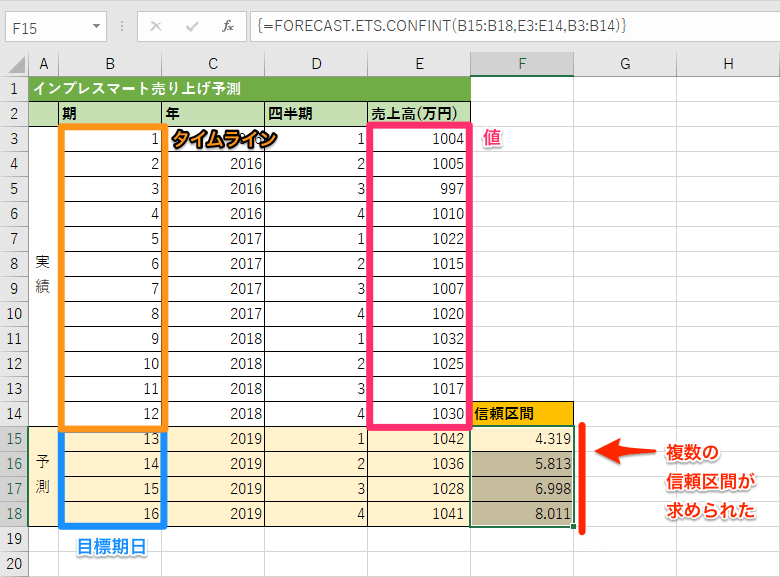
使用例2四半期ごとの売上高を元に2019年第1四半期〜第4四半期の売上高を予測し、その信頼区間を求める
{=FORECAST.ETS.CONFINT(B15:B18,E3:E14,B3:B14)}
上記はセルF15〜F18に入力されている数式です。FORECAST.ETS.CONFINT関数を配列数式として入力すれば、複数の［目標期日］の信頼区間が求められます。配列数式を入力するには、入力の終了時に［Enter］キーではなく［Ctrl］+［Shift］+［Enter］キーを押します。
活用のポイント
- 三重指数平滑法とは、過去のいくつかの値の平均から次の値を予測する方法です。このとき、最近の値のほうに指数関数的に大きなウェイトを与え、古い値の影響を少なくします。FORECAST.ETS.CONFINT関数では、季節による変動も含めて予測された値の信頼区間が求められます。
- ［目標期日］が［タイムライン］に指定された期よりも前の場合、［#NUM!］エラーとなります。
- ［タイムライン］には日付や「期」を表す値を指定します。［値］と［タイムライン］のサイズが異なる場合、［#N/A］エラーとなります。
- ［タイムライン］は並べ替えられている必要はありません。
- 季節性の変動を自動的に計算するには、［季節性］に1を指定するか省略します。ここでの例の周期は実際には4なので、［季節性］に4を指定しても、［季節性］を省略した場合と同じ結果になります。
- ［季節性］に8760を超える値を指定すると［#NUM!］エラーとなります。
- 欠測値がある場合には［補間］に1を指定するか省略します。［補間］に0を指定すると、欠測値が0と見なされます。
- ［季節性］と［補間］、［集計］の詳細については、FORECAST.ETS関数の記事を参照してください。
